Formeln för andragradsekvationer ser ut på följande sätt: 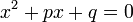
Ordet andragrads(ekvation) syftar på den högsta exponenten över funktionens variabel.
En variabel kan vara x, t, y, z, osv, notera att denna måste ej hela tiden vara x och att det kännetecknande för variabler är att de är förändliga.Tillskillnad från konstanter så som pi (p) som alltid har
ett värde p˜3,14), som i en andragradsekvation alltid är 2. Skulle exponenten över variabeln vara 1 så kallas funktionen för en förstagradsekvation,
skulle den vara tre så kallas den för en tredjegradsekvation och så vidare.
Det generella sättet att skriva en andragradsekvation på är följande:
, (a inte får vara lika med noll), av anledning att om a = 0 så kommer hela delen ax2 = 0 och då är det ingen andragradsekvation längre.
Nu undrar ni säkert var man har användning för något så annorlunda som detta, och den frågan ska ni få ett svar på: det är inte endast ett område,
utan flera! Allt ifrån geometri (Pytagorassats) till att beskriva en rörelse och för att exempelvis finna positionen hos en sten som kastas rakt upp i luften.
Tecknet a står för acceleration som är konstant (-9,82 m/), är starthastigheten för vilken man kastar stenen rakt upp på. Variabeln i formeln är t,
som står för tiden och är upphöjd i 2 en gång i formeln vilket gör den till en andragradsekvation. Känner man till accelerationen a, tiden t och hastigheten
när man kastar upp stenen kan man beräkna dess position.
För att kunna räkna ut detta, så krävs den välkände formeln ”PQ-formeln”, som ser ut på följande sätt:
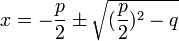
För att visa ett exempel har jag tagit fram en ekvation som jag sedan ska lösa med hjälp av PQ-Formeln:
Vi börjar med att skriva upp ekvationen
6x2 + 9x + 3 = 0
Få bort talet framför x2 genom att dividera allt med 6
x2 + 1.5x + 0.5 = 0 ( ÷6 )
Stoppa in alla värden i PQ-formeln
x = - (1.5 ÷ 2) ± v(1.5 ÷ 2)2 - 0.5
Lös uträkningarna till höger och vänster om ±-tecknet
x = -0.75 ± 0.25
Lös uträkningen
x1 = -0.5
x2 = -1
Vi avrundar
x1 ˜ -0.5
x2 ˜ -1
